Introduction to Pore Size & Flow in Porous Media

In porous plastics, pores are the solid surface openings through which gases, liquids, and smaller particles can flow. The morphology—size, shape, spatial arrangement, and connectivity of these pores—can significantly impact the movement of particles throughout a porous media. This article will outline the various types of pores, including their accessibility, impact on flow efficiency, measurement, and applicational implications.

Pore Connectivity and Porosity

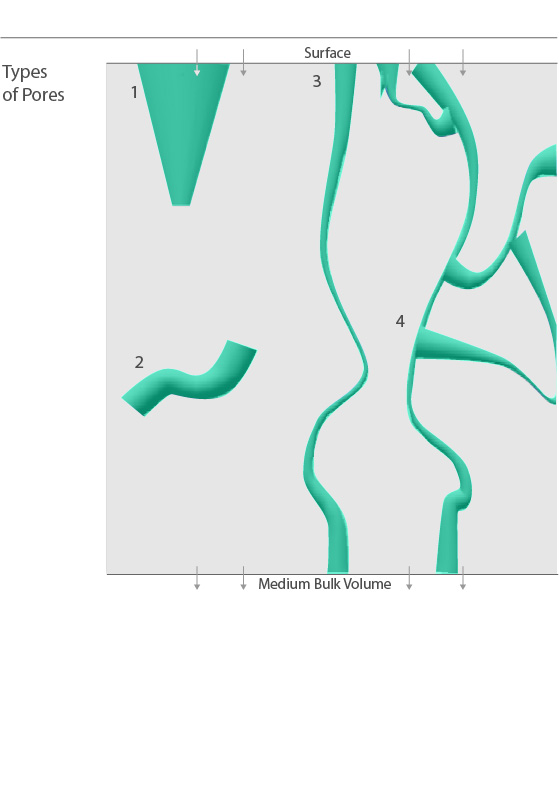
Flow within a porous media can be achieved only through a process of interconnectivity, meaning if a pore is not accessible from one or more ends, particles will fail to reach the bulk volume of the medium adequately. Closed porosity, also known as internal porosity, measures these void spaces that are not contributing to flow. The four types of pores are illustrated in the graphic to the right. They can be classified as blind pores (1), which are accessible only from one end, or isolated pores (2) which lack accessibility altogether. In contrast, interconnected pores (3 & 4) allow particle flow to occur from the surface all the way to the medium’s bulk volume. Open porosity, often called interconnected or effective porosity, is the measure of the pores contributing to actual flow, which is critically important in facilitating applications such as wicking and absorption, among others. Even for interconnected pores, however, overall efficiency can be heavily influenced by pore distribution, size, and tortuosity. Tortuosity is the geometric complexity of the interconnected pore structure. As illustrated to the right, pores with multiple ends (4) will exhibit higher levels of tortuosity, allowing flow to occur, but often with greater transit difficulty and time delay relative to more direct paths (3).

This chart shows the types of pores used in sintered porous plastic.

Introduction to Pore Size & Flow in Porous Media

Download

Applicational Significance of Pore Size

Applicational Significance of Pore Size Pore size and distribution are also critical parameters in determining the characteristics and performance of porous membranes. Pore size is the degree of space available for particle flow, while pore distribution is the relative abundance of each pore size to the medium’s volume. Per the International Union of Pure and Applied Chemistry (IUPAC), pore sizes are classified in one of three measurements:

Nanopore – pore size between 0.1 and 100 nm
Micropore – pore size between 0.1 and 100 μm
Millipore – pore size between 0.1 and 100 mm

Pore size substantially impacts properties that influence the regulation and movement of fluids. Absorption, or how much fluid a medium can store without leaking, is one of the most common – and critical – means of controlling liquids. Absorption can be seen in cleaning applications, where absorbing and trapping contaminants ensures a sterile, noncompromised environment, and in medical applications, where containing liquids like blood and exudations can mean the difference between life and death. As pore size becomes larger, so does the absorption rate of the media. Another application in which pore size influences efficiency is wicking.

Wicking is the speed and distance a fluid can travel within a porous media through capillary action (or capillary rise). Wicking refers to the ability of a liquid to flow upward through tight spaces via adhesion, cohesion, and surface tension rather than any applied external forces. The wicking process can be seen in many everyday products, such as clothing designed to wick sweat, marking pens that transfer ink onto a surface, and devices used to collect and test bodily fluids for rapid medical diagnoses.

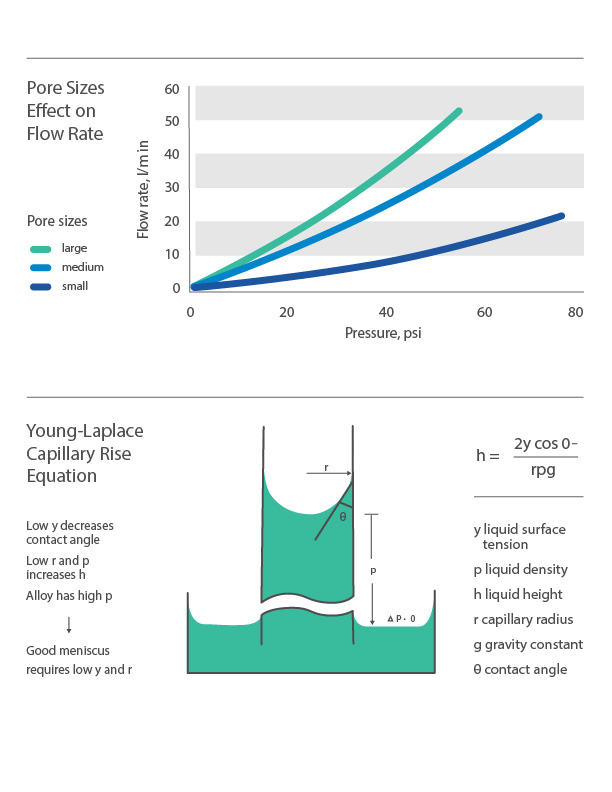
Using the Young-Laplace equation—an algebraic equation that defines the sustained capillary pressure difference between two static fluids, such as air and water—the height of capillary rise is proportional to pore size. Smaller pore size equates to faster wicking, while larger pore size will facilitate more absorption, reducing wicking speed and distance. Other significant pore size and distribution implications include emanation, pressure drop, and filtration efficiency.

Emanation is the liquid evaporation process at the surface, while pressure drop refers to the pressure loss between two porous media surfaces. Larger pore sizes will typically equate to higher emanation and less pressure drop. Smaller pore sizes, however, will improve the filtration efficiency of the media, increasing the percentage of retained particulates during fluid movement. Using a PMI Capillary Flow Porometer to capture data, the graph below illustrates that flow rate is always directly proportional to pore size at different applied pressure ranges.

This chart show the effect pore sizes has on flow rate as well as the Young-Laplace Capillary rise equation

Measuring Pore Size

Porosimetry is an analytical technique used to determine pore structure—particularly its size and distribution—by the intrusion of a liquid. Mercury Intrusion is a widely employed technique, especially in the petrochemical and catalyst industries, that uses a pressurized chamber to force mercury into pores typically sized between 3.2 nm and 400 μm. The pressure required for mercury intrusion to occur is inversely proportional to the size of the pores. For example, larger pores need less pressure for penetration, while smaller pores experience penetration as pressure increases. The volume of displaced mercury from these pores can be determined by measuring porosity and pore size. However, mercury intrusion is destructive by nature, and the sample is not recoverable once measurement has taken place.

Gas absorption can analyze a wide range of pore sizes, from 0.35 nm to 100 μm, which can be done accurately using vacuum-volumetric or gravimetric absorption techniques. To perform this measurement, a sample is collected and dosed with an absorbing gas under a range of predefined pressures. As volume difference is determined, a chart can be created to illustrate it as a function of pressure, which can then be used to determine pore size, volume, and surface area. Unlike mercury intrusion, the gas absorption process is not destructive to the sample. Capillary flow porometry is another pore size measurement technique based on the displacement of a wetting liquid under applied gas pressure. This method utilizes capillary effects to store a wetting fluid within a media’s pores typically ranging from 13 nm to 500 μm.

Using a completely wetted sample, gas pressure is increasingly applied until the capillary forces are overcome and the resulting gas flow increases can be measured. The large pores will empty first, while the smaller pores will continue to empty as pressure increases. In contrast to gas absorption and mercury intrusion, this method does not shed light on pore volume, only the diameters of the through pores. An alternative to capillary flow porometry is liquid-liquid displacement. This measurement is similarly conducted by introducing a wetting liquid to the porous sample; however, wetting liquid displacement is facilitated using a second immiscible liquid at increasing pressure. Because surface tension at the interface between the two liquids is lower than between the gas and liquid, this method is more effective in measuring smaller pore sizes without requiring high pressure.

Surface energy, a term used to describe the disruption of intermolecular bonds on a given surface, is another crucial factor to consider and is generally classified as high or low. When there is strong molecular attraction, a high surface energy is present, and water tends to spread or “wet out” the surface, which is necessary to form a strong bond. If there is low surface energy, the water tends to bead up instead of flowing out. The bonding surface and surface energy are vitally important when selecting any adhesive.

Controlling Pore Morphology

When designing a porous component, understanding the above principles is critical to addressing a product’s applicational challenges and requirements. Key areas of consideration, which build upon these fundamental understandings, include material selection, density of sintered or bonded goods, fiber size and orientation, and particle size and shape. Smaller particle and fiber sizes will provide smaller pores that allow for increased wicking speed and distance, while larger particles and fiber sizes will provide larger pores that increase absorption. Fiber orientation and increased density of the porous media can be designed to control the tortuosity of flow. Straight, parallel fibers improve flow, while random fiber orientation increases complexity and reduces flow efficiency.

Conclusion

Pore morphology can substantially impact a porous media’s filtration rate and efficiency. Interconnected pores, unlike blind or isolated pores, contribute to flow, but a variety of factors, including tortuosity, pore and particle size, density, and fiber orientation, among others, can impact their degree of transit efficiency. To create a tailored fluid transit solution with high efficiency, one must consider its intended applicational use, such as absorption or wicking, as well as any design constraints that may be present.

Download a PDF of this Article